Outline

• Introduction
• OLS estimation
• Inference
• Residual Analysis
• Robust Stadnard Error
• Endogeneity

Introduction

• Economic researchers are interested in the joint variation of all variables and the conditional variation of one of the variables related to the others.
• A linear relationship is a reasonable assumption.
  • Example 1：Mincer earnings function
  • Example 2: Cobb Douglas production function

Introduction

Example 5.1: Mincer earnings function (Mincer, 1958)

• : earnings,
• the intercept : initial earnings capacity,
• years of schooling
• years of potential labor market experience for individual .
• is the parameter of interest

Introduction

Example 5.2: Cobb Douglas production function (Cobb and Douglas, 1928)

• Cobb Douglas production:
• Apply a logarithmic transformation

• : output
• : capital
• labor
• The values of and are of particular interest.

OLS estimation: Model Setup

• Define the column vectors
  
• : the th row of .

OLS estimation: Model Setup

• LRM in matrix form

• Ordinary Least Squares (OLS) criterion

• OLS estimator of

OLS estimation

• We can interpret the regression coefficient as the marginal effect,

  • which is represented by for .

• An increase of one unit in will cause

  • the expected value of given to increase by the same amount,
  • while keeping all other factors constant.

• The relationship between a dependent variable and independent variables doesn't always have to be linear.

OLS estimation: Properties of OLS estimator

• The OLS estimator remains unbiased.

• Variance-covariance matrix has the form of

OLS Estimation

Use the dataset (data_incomeedu.dta) provided in the supplementary material to illustrate OLS estimation result in Python.

------------------------------------------------
variable name   type      variable label
------------------------------------------------
pid             int       pseudo ID (respondent)
village_pid     int       pseudo ID (village)
educ            int       years of education
income          float     income in 2020 (RMB) 
------------------------------------------------

OLS Estimation

import pandas as pd
import numpy as np
# 对应目录下从data_wageedu.dta中读取数据
data = pd.pandas.read_stata("dependency/data_incomeedu.dta")
x = data.loc[:,"educ"].to_numpy(dtype='float',
                                na_value=np.nan).reshape(-1,1)
y = data.loc[:,"income"].to_numpy(dtype='float',
                                na_value=np.nan).reshape(-1,1)
y = np.log(y)
X = np.append(np.ones((y.size,1)), x, axis=1)

OLS Estimation: Efficiency

import time
# 方法一：循环计算
def forloopols(x, y): 
    x_bar = x.mean() 
    y_bar = y.mean() 
    denominator = 0
    numerator = 0
    for i in range(y.size): 
        denominator += (x[i]-x_bar)**2
        numerator += (x[i]-x_bar)*(y[i]-y_bar)
    return numerator/denominator
# 方法二：矩阵计算
def matols(x, y): 
    X = np.append(np.ones((y.size,1)),x,axis=1)
    return np.matmul(np.matmul(np.linalg.inv(np.matmul(X.T,X)), X.T), y)[1]

startTime = time.time() # 计时开始
for k in range(1000):
    slope_v1, = forloopols(x, y)
endTime = time.time()-startTime # 计时结束
startTime = time.time()
for k in range(1000):
    slope_v2, = matols(x, y)
faster_rate = endTime/(time.time()-startTime) 
print("beta2 is estimated to be %5.3f by for-loop" 
      % (slope_v1))
print("beta2 is estimated to be %5.3f by matrix computation" 
      % (slope_v2))
print("Matrix computation is ", faster_rate," times faster.")

beta2 is estimated to be 0.039 by for-loop
beta2 is estimated to be 0.039 by matrix computation
Matrix computation is  34.75705486770159  times faster.

# 使用 np.dot()命令进行计算
print("By np.dot():",
      np.dot(np.dot(np.linalg.inv(np.dot(X.T,X)), X.T), y)[1])
# 使用 np.matmul()命令进行计算
print("By np.matmul():",
      np.matmul(np.matmul(np.linalg.inv(np.matmul(X.T,X)), X.T),
                y)[1])
# 使用 @ 命令进行计算
print("By @:",(np.linalg.inv(X.T @ X)@ X.T @ y )[1])

By np.dot(): [0.03915481]
By np.matmul(): [0.03915481]
By @: [0.03915481]

def timer_ols(method, rep_time=500000):
    startTime = time.time() # 计时开始
    if method == "dot":     # if条件为DOT的方法
        for ii in range(rep_time):
            np.dot(np.dot(np.linalg.inv(np.dot(X.T,X)), X.T), y)
        print("np.dot() takes %6.5f seconds" 
              % (time.time()-startTime) ) # 输出时长
    elif method == "matmul":# if条件为MATMUL的方法
        for ii in range(rep_time):
            np.matmul(np.matmul(np.linalg.inv(np.matmul(X.T,X)),
                                X.T), y)
        print("np.matmul() takes %6.5f seconds" 
              % (time.time()-startTime)) # 输出时长

    elif method == "at": # if条件为@的方法
        for ii in range(rep_time):
            (np.linalg.inv(X.T @ X) @ X.T) @ y
        print("@ takes %6.5f seconds" 
              % (time.time()-startTime)) # 输出时长
# 执行
timer_ols("dot")
timer_ols("matmul")
timer_ols("at")

np.dot() takes 13.22670 seconds
np.matmul() takes 10.44645 seconds
@ takes 10.75469 seconds

OLS Estimation

• To estimate , one could type

np.linalg.lstsq(X, y, rcond=None)[0]

array([[9.99572763],
       [0.03915481]])

• We can also estimate by using the StatsModels package.
• One can apply the statsmodels.OLS routine.
• add_constant() function could add the constant term directly into the covariates matrix.

OLS Estimation

import statsmodels.api as sm
X = sm.add_constant(x)
# 采用回归方程进行数据输入并进行拟合以及估计
result_ols = sm.OLS(y, X).fit()
print(result_ols.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.041
Model:                            OLS   Adj. R-squared:                  0.032
Method:                 Least Squares   F-statistic:                     4.778
Date:                Wed, 26 Jul 2023   Prob (F-statistic):             0.0309
Time:                        14:39:54   Log-Likelihood:                -96.436
No. Observations:                 115   AIC:                             196.9
Df Residuals:                     113   BIC:                             202.4
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          9.9957      0.159     62.705      0.000       9.680      10.312
x1             0.0392      0.018      2.186      0.031       0.004       0.075
==============================================================================
Omnibus:                       94.673   Durbin-Watson:                   1.053
Prob(Omnibus):                  0.000   Jarque-Bera (JB):             1055.552
Skew:                           2.642   Prob(JB):                    6.16e-230
Kurtosis:                      16.870   Cond. No.                         27.2
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

OLS Estimation

import matplotlib.pyplot as plt
beta = np.linalg.inv((X.T @ X))@ X.T @ y
plt.figure(figsize=(8,5))
plt.plot(x, y, 'ok', label='Original data', markersize=10)
plt.plot(x, beta[0] + beta[1]*x, 'gray', label='Fitted line')
plt.title("Figure 5.1: The OLS Fitted Line and the Original Data",
          fontsize=14)
plt.xlabel(r"$x$", fontsize=12)
plt.ylabel(r"$y$", fontsize=12)
plt.legend(fontsize=12)
plt.show()

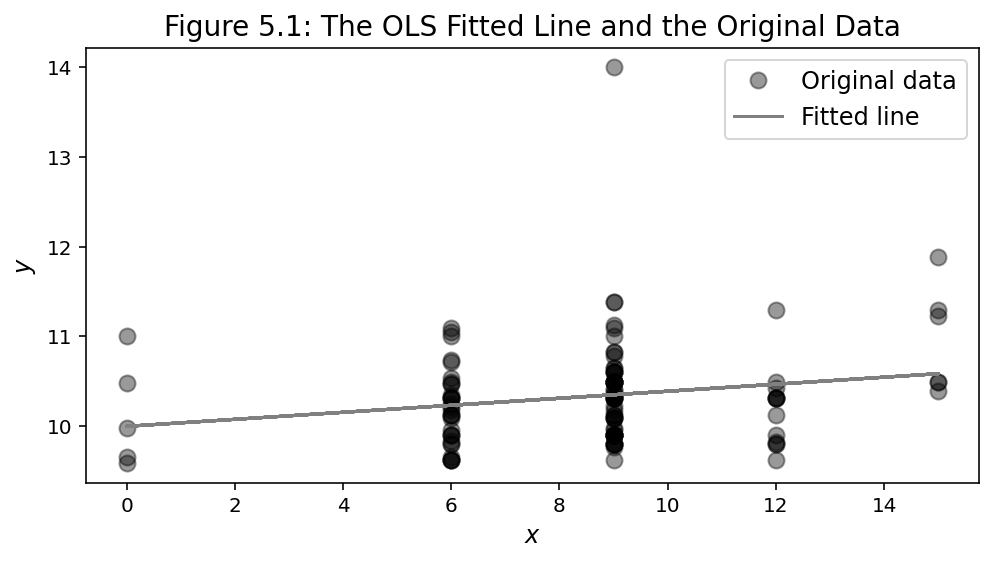
OLS Estimation

• As is an unknown, a consistent estimator

• Therefore, .

• One could compute the variance directly in Python based on this formula.

OLS Estimation

N = y.size
beta = np.dot(np.dot(np.linalg.inv(np.dot(X.T,X)), X.T), y)
e = y-np.dot(X,beta)
# 计算sigma平方的估计量
sigma2 = (1/(N-2)) * np.inner(e.T,e.T)
print("Estimate of sigma2:",sigma2[0])
# 计算OLS估计量方差矩阵
var = np.linalg.inv(np.dot(X.T,X))*sigma2
print("Variance-covariance matrix \n", var)
# 计算OLS估计量标准误
se = np.sqrt(np.diag(var))
print("Standard errors of beta0 is %6.3f and of beta1 is %6.3f" 
      % (se[0],se[1]))

OLS Estimation

    Estimate of sigma2: [0.31879951]
    Variance-covariance matrix 
     [[ 0.02541155 -0.00269516]
     [-0.00269516  0.00032085]]
    Standard errors of beta0 is  0.159 and of beta1 is  0.018

OLS Estimation

• Assessing goodness-of-fit in regression analysis.
• coefficient of determination, denoted as :

• TSS (total sum of squares), RSS (residual sum of squares), and ESS (error sum of squares) can be written in the following scalar notations

• The adjusted , denoted ,

OLS Estimation

# 定义M0矩阵
n = y.size
k = X.shape[1]
M0 = np.eye(n) - np.ones((n,n))/n
# 计算RSS,TSS与ESS
RSS = e.T@e
TSS = y.T@M0@y
# 计算R2与adj. R2
R2 = 1 - RSS/TSS
adjR2 = 1- (RSS/(n-k))/(TSS/(n-1))
print("R-squared: %5.4f" % (R2))
print("Adj. R-squared: %5.4f" % (adjR2))

R-squared: 0.0406
Adj. R-squared: 0.0321

OLS Estimation

To verify this equation, we can utilize the following code:

print("Adj. R-squared: %5.4f" % ((1- (n-1)*(1-R2)/(n-k))))

Adj. R-squared: 0.0321

Inferences

• Conducting a hypothesis test on a single restriction:

• is -distributed with degrees of freedom.

Consider again

• against the alternative that the impact does exist, i.e., .
• We have a conjecture that people with higher educational levels would earn more, so we anticipate rejecting the null hypothesis.

Inferences

print("t-stat of beta1: %4.3f"
      % ((beta.reshape(-1)/se)[1]) )

t-stat of beta1: 2.186

from scipy.stats import t
cv = t.ppf(0.975, df=N-2) # 临界值
lower_bounds = beta.reshape(-1) - se*cv
upper_bounds = beta.reshape(-1) + se*cv
print("95 CIs of beta1: [%5.3f, %5.3f]" % (lower_bounds[1],upper_bounds[1]))

95 CIs of beta1: [0.004, 0.075]

Inferences

• As we do not observe the error term , we can then use the OLS residual instead.

• -statistic can be constructed for a single element of , say ,

from scipy.stats import norm
# 计算S_x与S_ex
Sx = (X.T@X)/n
Q = np.diag(e.reshape(-1))**2
Sex = (X.T@Q@X)/n
# 计算渐近方差
Avar = np.linalg.inv(Sx)@Sex@np.linalg.inv(Sx)/n
Ase = np.sqrt(np.diag(Avar))
# 计算z统计量
zstat = beta.reshape(-1)/Ase
print("z-stat beta1 is %4.3f" % (zstat[1]) )
# 渐近置信区间
cv = norm.ppf(0.975)
lower_bounds = beta.reshape(-1) - Ase*cv
upper_bounds = beta.reshape(-1) + Ase*cv
print("95 asy. CIs of beta1 is [%5.3f,%5.3f]"
      % (lower_bounds[1],upper_bounds[1]))

z-stat beta1 is 2.223
95 asy. CIs of beta1 is [0.005,0.074]

Inferences

• . We first rewrite this hypothesis as .
• The restriction can be expressed as

R = [[1, -1]]
print(result_ols.f_test(R))

<F test: F=3185.238490556453, p=1.2527722221299107e-84, df_denom=113, df_num=1>

Residual Analysis

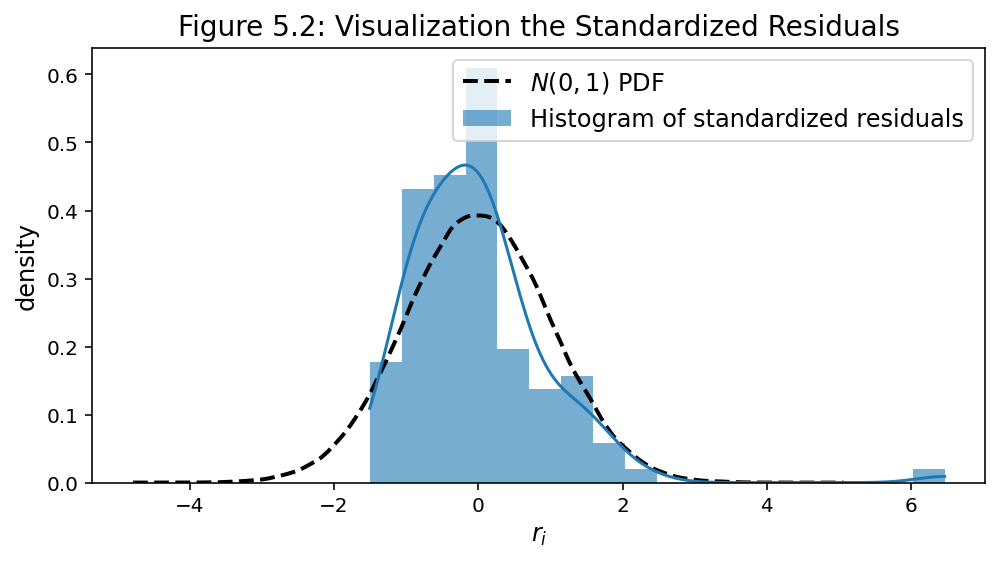
• The residual analysis allows us to check the adequacy of the model and detect outliers.
• It is common to study the distribution of residuals by plotting the histogram.
• Standardize residuals as , where
  • is the estimated standard error for .
• Then reconcile the plots with .

Residual Analysis

import seaborn as sns
# 标准化残差
sigma2_e = np.sqrt(np.sum(e**2)/(N-2))
r = e/sigma2_e
reference = np.random.normal(size=200000)

# 作图
plt.figure(figsize=(8,5))
sns.kdeplot(reference, color='k',
            label=r"$N(0,1)$ PDF", linestyle="--")
sns.histplot(r, kde=True, linewidth=0, color='gray',
             kde_kws={'cut':3}, stat='density',
             label=r"Standardized residuals $r_i$")
plt.title("Figure 5.2: Visualization the Standardized Residuals",
          fontsize=14)
plt.ylabel("density", fontsize=12)
plt.xlabel(r"$r_i$", fontsize=12)
plt.legend(loc="upper right", fontsize=12)
plt.show()

<><>

Residual Analysis: Test for the Normality

from scipy.stats import normaltest
k2, p = normaltest(r)
print("K2 statistic: %5.4f \np-value: %5.4f" % (k2,p))

K2 statistic: 94.6726 
p-value: 0.0000

Residual Analysis: Test for Heteroskedasticity

• A range of testing statistics to detect heteroscedasticity in the residuals.

• Examples Breusch-Pagan (BP) test (Breusch and Pagan, 1979) and the White test (White, 1980).

• is (homoscedasticity), but one of the possibilities is that

Residual Analysis: Test for Heteroskedasticity

• Test for heteroskedasticity means that all slope coefficients are equal to zero.
• This involves testing if .
  • The intercept equals under this constraint.
• As we cannot observe , we substitute it with OLS residuals.

Residual Analysis: Test for Heteroskedasticity

from statsmodels.stats.diagnostic import het_breuschpagan, het_white
model = sm.OLS(y, X).fit()
bp_result = het_breuschpagan(model.resid, X)
white_result = het_white(model.resid, X)
print('BP test p-value: '+str(bp_result[3]))
print('White test p-value: '+str(white_result[3]))

BP test p-value: 0.6762218491291369
White test p-value: 0.9152386628311834

Robust Standard Errors: White Standard Errors

• The errors are most likely heteroskedastic.
• One common technique is to use the White standard errors (White, 1980).
• These are also known as
  • heteroskedasticity-robust standard errors,
  • or Eicker-Huber-White standard errors

Consider the formula:

We code in Python next.

Robust Standard Errors

# 计算Omega
omega_hat = (e@e.T)*n/(n-k)
# 计算稳健方差矩阵
XXinv = np.linalg.inv(X.T@X)
var = XXinv@X.T@np.diag(np.diag(omega_hat))@X@XXinv
print("White variance-covariance matrix \n", var)
# 计算稳健标准误
se = np.sqrt(np.diag(var))
print("White standard errors of beta0 is %6.5f and of beta1 is %6.5f" 
      % (se[0],se[1]))

White variance-covariance matrix 
 [[ 0.02255978 -0.00250354]
 [-0.00250354  0.00031564]]
White standard errors of beta0 is 0.15020 and of beta1 is 0.01777

Robust Standard Errors: Clustered Standard Errors

• clustered standard errors are widely used in a variety of applied econometric settings.
• The sample consists of survey responses from 110 individuals across 8 randomly selected villages in Guangdong Province.
• 8 villages can be situated in different areas of Guangdong. Therefore, it is likely that respondents from more developed villages have a higher income compared to those from less developed ones.

Call Stata from Python

# 配置Python-Stata交互
import os
os.chdir('/Applications/Stata/utilities')
from pystata import config
config.init('mp')
# 将数据传输至Stata
from pystata import stata
stata.pdataframe_to_data(data, force=True)
# 回归并使用聚类标准误
stata.run(
    '''gen lincome = ln(income)
    regress lincome educ, cluster(village_pid)
    ''')

Linear regression                      Number of obs     =        115
                                       F(1, 7)           =       9.80
                                       Prob > F          =     0.0166
                                       R-squared         =     0.0406
                                       Root MSE          =     .56462

                   (Std. err. adjusted for 8 clusters in village_pid)
---------------------------------------------------------------------
        |               Robust
lincome | Coefficient  std. err.    t    P>|t|   [95% conf. interval]
--------+------------------------------------------------------------
   educ |   .0391548   .0125084   3.13   0.017   .0095772    .0687324
  _cons |   9.995728   .1576285  63.41   0.000   9.622995    10.36846
---------------------------------------------------------------------

Robust Standard Errors: Clustered Standard Errors

• For the LRM, the cluster standard errors can be expressed as

• is the number of clusters,
• is a block diagonal matrix defined based on , with unrestricted values in each block of the cluster but zeros elsewhere.
• is a finite sample adjustment term.

Robust Standard Errors: Clustered Standard Errors

# 从数据中获取cluster变量
cluster = data.loc[:,"village_pid"].to_numpy(dtype='float',
                                            na_value=np.nan).reshape(-1,1)
G = len(np.unique(cluster))
# 计算聚类方差的Omega
omega_hat = (e@e.T)*((G)/(G-1))*((n-1)/(n-k))
omega_hat_c = np.copy(omega_hat)
for i in range(n):
    for j in range(n):
        if i>j:
            if cluster[i]!=cluster[j]:
                omega_hat_c[i,j] = 0
                omega_hat_c[j,i] = 0

# 计算聚类方差矩阵
XXinv = np.linalg.inv(X.T@X)
var = XXinv@X.T@omega_hat_c@X@XXinv
print("Clustered variance-covariance matrix \n", var)
# 计算聚类标准误
se = np.sqrt(np.diag(var))
print("Clustered standard errors of beta0 is %6.5f and of beta1 is %6.5f" 
      % (se[0],se[1]))

Clustered variance-covariance matrix 
 [[ 0.02484674 -0.00062565]
 [-0.00062565  0.00015646]]
Clustered standard errors of beta0 is 0.15763 and of beta1 is 0.01251

Endogeneity

• When studying the return of education problems, the economic literature (Mroz, 1987; Card, 1993) usually employ a linear model to estimate the impact of years of schooling () on the wage ():

• The OLS estimator is biased. This bias is known as omitted variable bias.

• Omitted variables that are correlated with dependent and independent variables
• Independent variables is measured with error
• Dependent and independent variables that are simultaneously determined.

Endogeneity: IV Estimations

• To conduct IV estimations, IV variables meet two conditions:
  • IV exogeneity: IV variables are uncorrelated with the error term.
  • IV relevance : IV variables should be partially and sufficiently strongly correlated with the endogeneous variable once the other independent variables are controlled for.

Endogeneity: Just-identified Case

• We cannot assume that the is uncorrelated with .

• IV conditions are represented as: but .

• Since and , we obtain

Endogeneity: Just-identified Case

• The IV estimator of can be constructed using the sample analogues of the covariances

• Define and . In the matrix form, the IV estimator of is

Endogeneity: Just-identified Case

• is a consistent estimator and its asymptotic variance can be estimated by

• with .
• Note that this estimator is valid under homoskedasticity. We will discuss heteroskedastic case later.

Endogeneity: Just-identified Case

import wooldridge
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
# 读取数据包当中的MORZ原始数据
reduc_women = wooldridge.data('mroz')
# 去掉数据中工资为空的观测值
datas = reduc_women.dropna(subset=['lwage'])
x=datas[['exper','expersq','educ']]
y=datas.loc[:,'lwage']
X = sm.add_constant(x)
# OLS估计法（不处理内生性问题）
result_ols = sm.OLS(y, X).fit()
print(result_ols.summary2())

                Results: Ordinary least squares
=================================================================
Model:              OLS              Adj. R-squared:     0.151   
Dependent Variable: lwage            AIC:                871.1979
Date:               2023-11-15 17:58 BIC:                887.4344
No. Observations:   428              Log-Likelihood:     -431.60 
Df Model:           3                F-statistic:        26.29   
Df Residuals:       424              Prob (F-statistic): 1.30e-15
R-squared:          0.157            Scale:              0.44412 
-------------------------------------------------------------------
           Coef.    Std.Err.      t      P>|t|     [0.025    0.975]
-------------------------------------------------------------------
const     -0.5220     0.1986   -2.6282   0.0089   -0.9125   -0.1316
exper      0.0416     0.0132    3.1549   0.0017    0.0157    0.0675
expersq   -0.0008     0.0004   -2.0628   0.0397   -0.0016   -0.0000
educ       0.1075     0.0141    7.5983   0.0000    0.0797    0.1353
-----------------------------------------------------------------
Omnibus:             77.792       Durbin-Watson:          1.961  
Prob(Omnibus):       0.000        Jarque-Bera (JB):       300.917
Skew:                -0.753       Prob(JB):               0.000  
Kurtosis:            6.822        Condition No.:          2212   
=================================================================
* The condition number is large (2e+03). This might indicate
strong multicollinearity or other numerical problems.

Endogeneity: IV Estimations

y = datas[['lwage']].to_numpy()
X = sm.add_constant(datas[['exper','expersq','educ']]).to_numpy()
Z = sm.add_constant(datas[['exper','expersq',
                           'fatheduc']]).to_numpy()
# IV点估计
beta_IV = np.linalg.inv(Z.T@X)@Z.T@y
# 方差估计
e =  y-X@beta_IV
# 计算sigma平方的估计量
sigma2 = (1/(y.size)) * np.inner(e.T,e.T)
se_IV = np.sqrt(np.diag(np.linalg.inv(Z.T@X)@Z.T
                        @Z@np.linalg.inv(X.T@Z)*sigma2))

Endogeneity: IV Estimations

# 汇报结果
print("          Parameter  Std. Err.")
print("Intercept %8.4f, %8.4f" 
      % (beta_IV[0], se_IV[0]) )
print("exper     %8.4f, %8.4f" 
      % (beta_IV[1], se_IV[1]) )
print("expersq   %8.4f, %8.4f" 
      % (beta_IV[2], se_IV[2]) )
print("educ      %8.4f, %8.4f" 
      % (beta_IV[3], se_IV[3]) )

          Parameter  Std. Err.
Intercept  -0.0611,   0.4344
exper       0.0437,   0.0133
expersq    -0.0009,   0.0004
educ        0.0702,   0.0343

Endogeneity: IV Estimations

from linearmodels.iv import IV2SLS
reg_2sls=IV2SLS.from_formula(
         formula='lwage~1+exper+expersq+[educ~fatheduc]',
         data= datas)
print(reg_2sls.fit(cov_type='unadjusted'))

                   IV-2SLS Estimation Summary                  
===================================================================
Dep. Variable:                lwage   R-squared:             0.1430
Estimator:                  IV-2SLS   Adj. R-squared:        0.1370
No. Observations:               428   F-statistic:           25.176
Date:              Wed, Nov 15 2023   P-value (F-stat)       0.0000
Time:                      17:57:30   Distribution:         chi2(3)
Cov. Estimator:          unadjusted                                
                                                                   
                       Parameter Estimates                  
===================================================================
         Parameter  Std. Err.   T-stat  P-value  Lower CI  Upper CI
-------------------------------------------------------------------
Intercept  -0.0611     0.4344  -0.1407   0.8881   -0.9125    0.7903
exper       0.0437     0.0133   3.2744   0.0011    0.0175    0.0698
expersq    -0.0009     0.0004  -2.2107   0.0271   -0.0017   -0.0001
educ        0.0702     0.0343   2.0485   0.0405    0.0030    0.1374
===================================================================
Endogenous: educ 
Instruments: fatheduc 
Unadjusted Covariance (Homoskedastic) 
Debiased: False

Endogeneity: 2SLS Estimation

• is a projection of with , i.e.,

• the projection matrix is symmetric and idempotent (i.e., ).
• We use as instruments for and apply the IV estimation as in

Endogeneity: 2SLS Estimation

The two-step procedure can be described as:

1. Obtain by estimating an OLS against all of exogenous variables, including all of instruments (the first-stage regression).

2. Use in place of to estimate against and all of exogenous independent variables, not instruments (the second stage regression).

We can just estimate 2SLS estimators in one step by using and . This is also what other econometrics packages do.

Endogeneity: 2SLS Estimation

Z = sm.add_constant(datas[['exper','expersq','fatheduc',
                           'motheduc']]).to_numpy()
# 2SLS点估计
Pz = Z@np.linalg.inv(Z.T@Z)@Z.T
Xhat = Pz@X
beta_2SLS = np.linalg.inv(Xhat.T@X)@Xhat.T@y

Endogeneity: 2SLS Estimation

• The variance (or standard errors) produced by the two-step procedure are incorrect and tend to be smaller than the actual ones.
• The correct variance (under homoskedastric assumption)

• with .

• The heteroskedasticity-robust (White) standard errors is

• .

Endogeneity: 2SLS Estimation

# 方差估计
e =  y-X@beta_2SLS
# 计算sigma平方的估计量
diagomega =  np.diag(np.diag(e@e.T))
se_2SLS = np.sqrt(np.diag(np.linalg.inv(Xhat.T@Xhat)
                          @(Xhat.T@diagomega@Xhat)
                          @np.linalg.inv(Xhat.T@Xhat)  ))
print("          Parameter  Robust Std. Err.")
print("Intercept %8.4f, %8.4f" 
      % (beta_2SLS[0], se_2SLS[0]) )
print("exper     %8.4f, %8.4f" 
      % (beta_2SLS[1], se_2SLS[1]) )
print("expersq   %8.4f, %8.4f" 
      % (beta_2SLS[2], se_2SLS[2]) )
print("educ      %8.4f, %8.4f" 
      % (beta_2SLS[3], se_2SLS[3]) )

          Parameter  Robust Std. Err.
Intercept   0.0481,   0.4278
exper       0.0442,   0.0155
expersq    -0.0009,   0.0004
educ        0.0614,   0.0332

from linearmodels.iv import IV2SLS 
reg_2sls=IV2SLS.from_formula(
         formula='lwage~1+exper+expersq+[educ~motheduc+fatheduc]',
         data= datas)
print(reg_2sls.fit())

                   IV-2SLS Estimation Summary                  
===================================================================
Dep. Variable:                lwage   R-squared:             0.1357
Estimator:                  IV-2SLS   Adj. R-squared:        0.1296
No. Observations:               428   F-statistic:           18.611
Date:              Wed, Nov 15 2023   P-value (F-stat)       0.0003
Time:                      17:58:25   Distribution:         chi2(3)
Cov. Estimator:              robust                                
                                                                   
                       Parameter Estimates                  
===================================================================
         Parameter  Std. Err.   T-stat  P-value  Lower CI  Upper CI
-------------------------------------------------------------------
Intercept   0.0481     0.4278   0.1124   0.9105   -0.7903    0.8865
exper       0.0442     0.0155   2.8546   0.0043    0.0138    0.0745
expersq    -0.0009     0.0004  -2.1001   0.0357   -0.0017   -0.0001
educ        0.0614     0.0332   1.8503   0.0643   -0.0036    0.1264
===================================================================
Endogenous: educ
Instruments: fatheduc, motheduc
Unadjusted Covariance (Heteroskedastic)
Debiased: False

Endogeneity: Testing for IV Validity

• The first-step estimation of the 2SLS method can be used to test for the IV relevance.
• Conduct an -test on all instruments to see if they are jointly significant in the endogenous variable.

#第一阶段回归
reg_1stage=smf.ols(formula='educ~exper+expersq+fatheduc',
                   data=datas)
results_1stage=reg_1stage.fit()
print(results_1stage.summary2())

                 Results: Ordinary least squares
==================================================================
Model:              OLS              Adj. R-squared:     0.170    
Dependent Variable: educ             AIC:                1846.5075
Date:               2023-11-15 19:53 BIC:                1862.7440
No. Observations:   428              Log-Likelihood:     -919.25  
Df Model:           3                F-statistic:        30.09    
Df Residuals:       424              Prob (F-statistic): 1.18e-17 
R-squared:          0.176            Scale:              4.3366   
-------------------------------------------------------------------
                Coef.   Std.Err.     t     P>|t|    [0.025   0.975]
-------------------------------------------------------------------
Intercept       9.8870    0.3956  24.9920  0.0000   9.1094  10.6646
exper           0.0468    0.0411   1.1391  0.2553  -0.0340   0.1276
expersq        -0.0012    0.0012  -0.9364  0.3496  -0.0036   0.0013
fatheduc        0.2705    0.0289   9.3670  0.0000   0.2137   0.3273
------------------------------------------------------------------
Omnibus:               10.235       Durbin-Watson:          1.919 
Prob(Omnibus):         0.006        Jarque-Bera (JB):       17.236
Skew:                  -0.103       Prob(JB):               0.000 
Kurtosis:              3.961        Condition No.:          1411  
==================================================================
* The condition number is large (1e+03). This might indicate
strong multicollinearity or other numerical problems.

Endogeneity: Testing for IV Validity

• In the case of having more instrumental variables than endogenous variables,
  • which is known as the over-identified case,
• We can use the over-identification test to confirm this requirement.

• The intuition:
  • if we have two valid instruments, such as and ,
  • we can compute two separate estimators.
• If these estimators are significantly different from each other,
  • it indicates that at least one of the instrumental variables is invalid.

Endogeneity: Testing for IV Validity

from scipy.stats import chi2
# 1. 2SLS回归，并计算残差项
reg_2sls=IV2SLS.from_formula(
         formula='lwage~1+exper+expersq+[educ~fatheduc+motheduc]',
         data=datas)
results_2sls=reg_2sls.fit(cov_type='unadjusted', debiased=True)
# 2. 残差对工具变量与外生变量回归
datas['resid_2sls']=results_2sls.resids
# 3.1 检验OR所需要的回归构建
reg_or=smf.ols(formula='resid_2sls~ 1+exper+expersq+motheduc+fatheduc', data=datas)
results_or=reg_or.fit()

Endogeneity: Testing for IV Validity

# 3.2 统计检验得出结论
R2 = results_or.rsquared
n  = results_or.nobs     
q  = 2-1
teststt=n*R2
pval=1-chi2.cdf(teststt,q)
print(f'Overidentification test: {teststt}')
print(f'p-value: {pval}')
print(f'sample size: {n}')

Overidentification test: 0.3780713419639192
p-value: 0.5386372330714363
sample size: 428.0

Endogeneity: Testing for Endogeneity

# 第一阶段回归
reg_1stage=smf.ols(formula='educ~exper+expersq+motheduc+fatheduc',
                   data=datas)
results_1stage=reg_1stage.fit()
# 从计算结果中提取残差项
datas['resid']=results_1stage.resid
# 将残差项加入OLS模型
reg_endo=smf.ols(formula='lwage~resid+educ+exper+expersq',data=datas)
results_endo=reg_endo.fit()
print(results_endo.summary2())

                 Results: Ordinary least squares
=================================================================
Model:              OLS              Adj. R-squared:     0.154   
Dependent Variable: lwage            AIC:                870.3816
Date:               2023-11-15 20:15 BIC:                890.6772
No. Observations:   428              Log-Likelihood:     -430.19 
Df Model:           4                F-statistic:        20.50   
Df Residuals:       423              Prob (F-statistic): 1.89e-15
R-squared:          0.162            Scale:              0.44225 
------------------------------------------------------------------
               Coef.   Std.Err.     t     P>|t|    [0.025   0.975]
------------------------------------------------------------------
Intercept      0.0481    0.3946   0.1219  0.9030  -0.7275   0.8237
resid          0.0582    0.0348   1.6711  0.0954  -0.0103   0.1266
educ           0.0614    0.0310   1.9815  0.0482   0.0005   0.1223
exper          0.0442    0.0132   3.3363  0.0009   0.0181   0.0702
expersq       -0.0009    0.0004  -2.2706  0.0237  -0.0017  -0.0001
-----------------------------------------------------------------
Omnibus:             74.968       Durbin-Watson:          1.931  
Prob(Omnibus):       0.000        Jarque-Bera (JB):       278.059
Skew:                -0.736       Prob(JB):               0.000  
Kurtosis:            6.664        Condition No.:          4419   
=================================================================